EnsembleLearning

Posted on Edited on In Views:

[toc]

last:2019-09-04 21:45:21

update: 2020-06-20

Voting：利用投票做分类

  • hard-voting：多个分类器的结果中选择重合数目最多的。

  • Soft-voting：会对预测的结果配上权重，使得预测结果最好的类别更大概率视为正确的。

  • 比如用LR、SVM、随机森林等模型组合在一起进行投票：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    from sklearn.ensemble import RandomForestClassifier
    from sklearn.ensemble import VotingClassifier
    from sklearn.linear_model import LogisticRegression
    from sklearn.svm import SVC

    log_clf = LogisticRegression(solver="lbfgs", random_state=42)
    rnd_clf = RandomForestClassifier(n_estimators=100, random_state=42)
    svm_clf = SVC(gamma="scale", random_state=42)

    voting_clf = VotingClassifier(
        estimators=[('lr', log_clf), ('rf', rnd_clf), ('svc', svm_clf)],
        voting='hard')

    """ Soft-voting
    voting_clf = VotingClassifier(
        estimators=[('lr', log_clf), ('rf', rnd_clf), ('svc', svm_clf)],
        voting='soft')
    """


    voting_clf.fit(X_train, y_train)
    from sklearn.metrics import accuracy_score

    for clf in (log_clf, rnd_clf, svm_clf, voting_clf):
        clf.fit(X_train, y_train)
        y_pred = clf.predict(X_test)
        print(clf.__class__.__name__, accuracy_score(y_test, y_pred))
        
    ## voting的结果比单个分类器好
    LogisticRegression 0.864
    RandomForestClassifier 0.896
    SVC 0.896
    VotingClassifier 0.912

  • 背后原理：Law of large numbers：

  • 前提：分类器独立，学习到的错误模式各不相同。

这一种做法是使用不同的分类器算法，

另一种做法是在不同的训练集上训练分类器。

Bagging：（Bootstrap aggregating）：有放回采样训练集

  • Pasting：不放回。。
1
2
3
4
5
6
7
from sklearn.ensemble import BaggingClassifier 
from sklearn.tree import DecisionTreeClassifier

# 等于随机森林
#500个决策树的bagging，每个采样为max_samples（可设为【0，1】作为百分比），n_jobs=-1使用全部cpu
bag_clf = BaggingClassifier( DecisionTreeClassifier(), n_estimators=500, max_samples=100, bootstrap=True, n_jobs=-1)
bag_clf.fit(X_train, y_train) y_pred = bag_clf.predict(X_test)

  • Out-of-Bag Evaluation：bagging里面没被采样的训练集上的验证预测：

    1
    2
    3
    >>> bag_clf.fit(X_train, y_train)
    >>> bag_clf.oob_score_
    0.90133333333333332

Extra variant methods：

​ Random Subspaces method（Sampling features ）、

​ Random patches method（Sampling features and training instances）

特征重要性显示：

1
2
3
4
5
6
7
8
9
10
11
12
from sklearn.datasets import load_iris
iris = load_iris()
rnd_clf = RandomForestClassifier(n_estimators=500, random_state=42)
rnd_clf.fit(iris["data"], iris["target"])
for name, score in zip(iris["feature_names"], rnd_clf.feature_importances_):
    print(name, score)

###   
sepal length (cm) 0.11249225099876374
sepal width (cm) 0.023119288282510326
petal length (cm) 0.44103046436395765
petal width (cm) 0.4233579963547681

Boosting

做法：Train predictors sequentially，each trying to correct its predecessor.

AdaBoost：给每个训练样本学习一个权重

做法：先用base classifier在训练集上分类，对分类错误的样本增加它们的权重，然后下一个base classifier继续训练集上做分类，更新权重。上述过程也对每个base classifier学到一个权重， 预测的时候，把所有分类器的预测权重结合起来做预测。

Gradient Boosting

overview

  • 泛化性：用偏差与方差分解理解泛化性；
  • 利用bagging降低方差；利用boosting降低偏差；

集成方法总览：

  1. predictor的决策被联合在一起用来对新样本做决策，如voting；

  2. 为了使每个预测器（predictor）不一样，它们应该学习不一样的学习假设（hypotheses）

    有四类方法使得预测器的学习假设不一样：

    1. 不同的算法；
    2. 不同的超参数选择；
    3. 训练不同的数据；
    4. 对训练样本采用不同权重的训练；

  3. 集成学习的难点在于如何选择上述的集成目标。

  • bagging方法：在训练集的随机子集上独立的训练每一个分类器；
  • boosting方法：把分类器序列化的做训练，每一次的训练更关注上一轮训练中预测错误的样本。
  • 上面的两个算法各有不同，通过学习算法的偏差和方差理论来作分析。

方差偏差理论

可以通过KNN算法看到一种现象，不同的K的选择使得模型太简单，那么可能与数据形成欠拟合；也可能使得模型过于复杂，那么可能与数据形成过拟合；那么如何量化这种现象，那就是方差偏差理论。

增大$k$ 使得方差下降但是偏差增加，减小$k$使得方差增大但是偏差下降。随着$k$的增加，方差减小了；但是如果我们增加太多$k$，那么我们就不再沿着真正的边界线，我们观察到高偏差。

  • 高偏差低方差图：$k$值大的时候，平均预测值离真实值比较远，但是方差比较小，预测的结果比较集中。

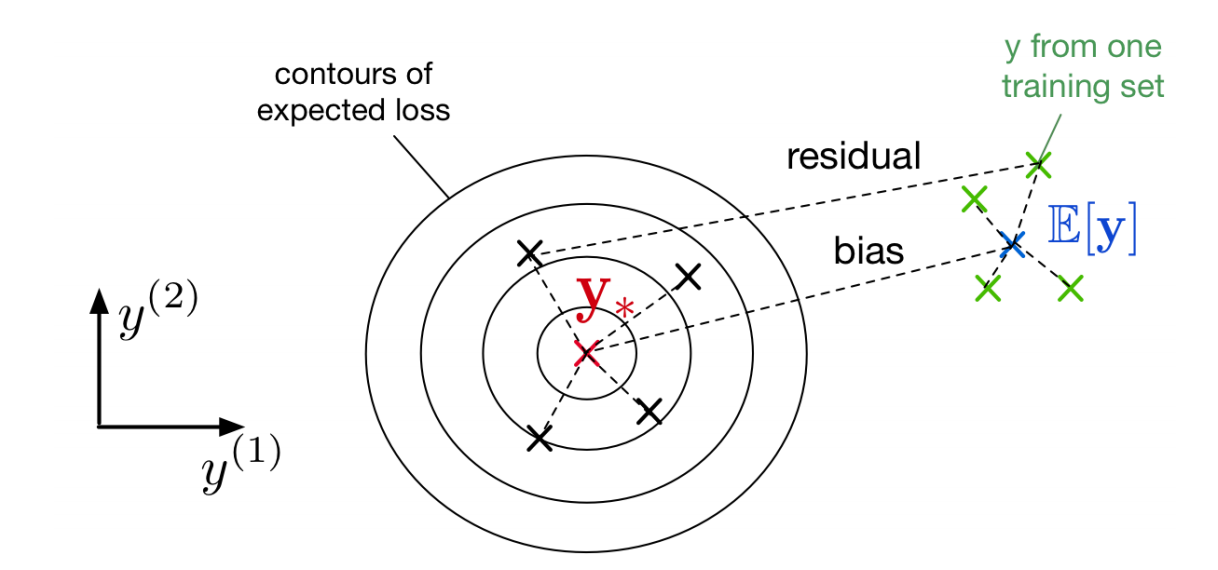
高偏差低方差

  • 低偏差高方差图：$k$ 值小的时候，平均预测值离真实值比较近，但是方差太大，每一次的预测值波动性很大。

低偏差高方差

先从一个例子出发：

（1）假设训练集由$N$ 对样本组成，每个样本独立同分布地抽取于数据生成分布 $P_{\text{(data)}}$ ,

​ 整个训练数据集的诱导分布（induced distribution）表示为 $P_{\text{(train)}}$.

（2）取一个固定的测试点$X$，然后做这么一个实验，我们不断的从 $P_{\text{(train)}}$里独立地采样多次训练数据集；

（3）我们的学习算法在每一个训练数据集$D$上做训练，产生一个分类器 $h_D$；然后对每一个分类器我们对刚才取的点做分类有 $h_D(X)=y$；

(4) 结论是 $y$，一个样本的类别，成了随机变量；原因是 $D$是随机的，因此分类器 $h_D$ 是随机的，因此它的预测$h_D(X)$也是随机的；

因为 $y=h_D(X)$ 是随机变量，

我们可以讨论它在训练集$P_{\text{(train)}} $ 的期望和方差！

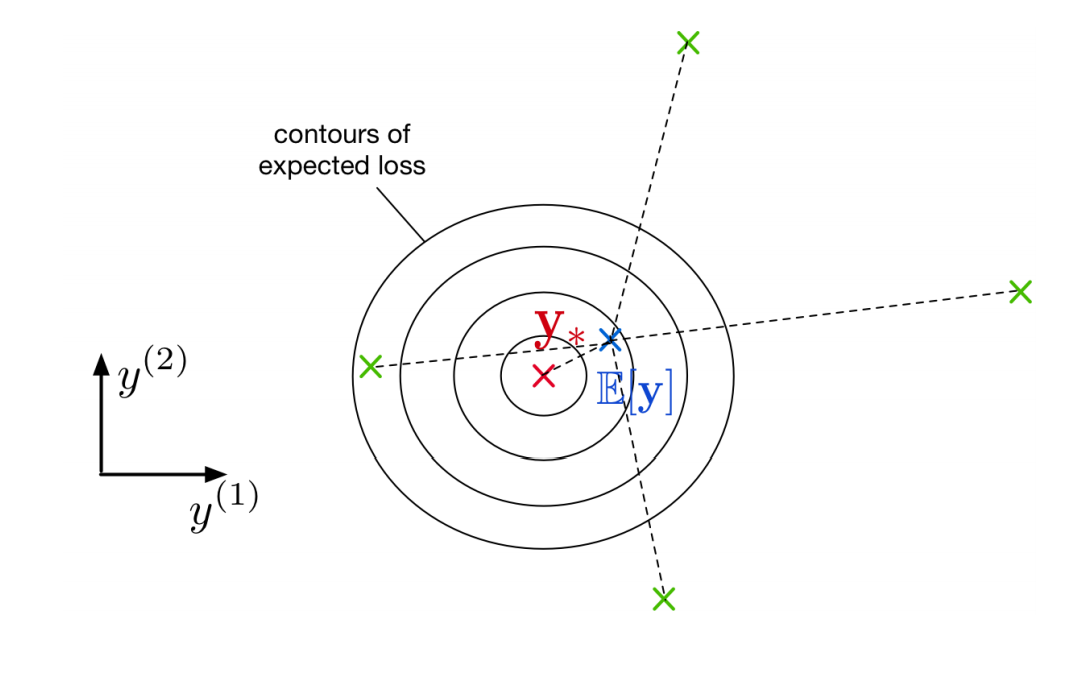
如下图：

  • 上图中，假设了给定了$X$的情况，$t$ 是确定的；
  • 看出来对不同的数据集，存在一个对$X$的期望损失：
  • 每一个数据点$X$ 的期望损失是不同的，

现在假设$L$是均方误差$L(y, t) = \frac{1}{2} (y - t)^2$，对上面的期望损失做分解：

★：注意最后一步的时候， $\mathbb E_{(X,D)}$ 是数据集 $D$ 与测试样本点 $X$ 都是随机变量计算平均值，

$h_D(X)$ 是对任何测试$X$都有一个训练值，它的随机变量只有训练集 $D$ ；

因此对随机变量 $D$ 取期望之后化为 $\mathbb E_{D}[h_D(X)]$ ，

其他的值都不是变量$D$的函数，因此保持原样，最后得到的第一项为方差(Variance)，第二项为偏差(Bias)。

  • 偏置：平均来说，我们的分类器离真实目标有多近；（对应于underfitting）
  • 方差：当我们生成新的数据集时，我们的预测有多分散? (对应于overfitting)

偏置：由公式看出，偏置是在一个固定的预测器下，训练集是随机变量，对所有可能的训练集的训练结果取均值，然后与真实值的误差；当然对所有预测值与真实值的误差都取均值。

方差：有公式看出，训练集不一样时，预测的结果离对所有数据上的平均预测结果偏离的均值。

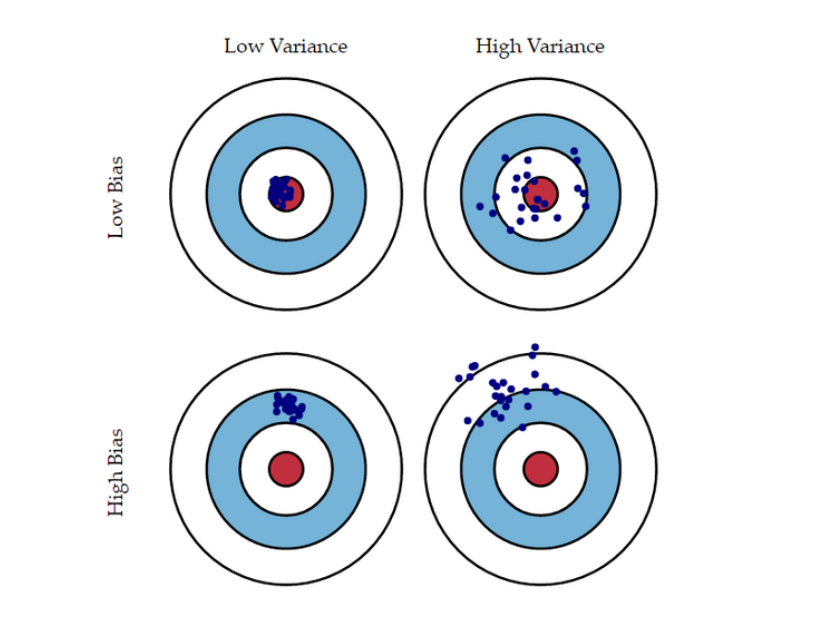
  • 下图：投掷飞镖=对数据集的每次采样进行预测。看出来高bias的时候，数据的预测值离真实值都比较远，低bias的时候都离真实值比较近；高bias明显欠拟合更多；然后是低variance的时候，预测值都比较集中，高variance的时候预测值都比较分散；高variance明显说明了过拟合的情况，生成不同的数据，预测值也大范围的在变化，即泛化性差，太拟合训练数据（上一次或前几次投飞镖的位置作为训练数据，但是这次投飞镖的结果（测试）却与训练结果差很远）了。

投掷飞镖=对数据集的每次绘制进行预测

Bagging: Motivation

假设我们可以从$P_{\text{(train)}}$ 里独立地采样$m$次，作为$m$ 个独立的训练集，

在每个训练集上我们可以训练$m$个预测器(predictor)： $hi=h{(D_i)}$

对所有的预测器的结果求平均得到 $h=\frac{1}{m}\sum_{i=1}^mh_i$ 。推导这个 $h$ 是怎么影响bias和variance的：

  • 对bias没有影响：因为平均预测具有相同的期望

对所有数据集 $D_1,…,D_m$ 作为变量$D$的值，求该变量的均值，

由期望公式 $E(X)=\sum_{i} p_i x_i$ 得到中间式子，然后写成最后的式子形式。

  • 方差下降了：因为我们对独立样本的方差联合在一起求了均值，得到最后的方差：方差公式$\text{Var}(aX) = a^2\text{Var}(X)$, 因此，第二式的每一项前面的系数都是$\frac{1}{m^2}$，然后求平均方差值。

Bagging: Idea

上面的分析说明了问题所在，只要有很多独立的数据集那么我的结果肯定会很好，因为我可以训练很多预测器然后综合起来，减小方差啊！~

但是现实是残酷的，如下：

  1. 我们往往得不到数据生成分布$P_{(data)}$；
  2. 收集独立的大量数据集是耗费资源的；

基于这样的情况，Bagging（或称为bootstrap aggregation）算法怎么考虑的呢？

我只有一个训练集$D$，里面有$n$个样本；好，这样的话，我利用$D$生成$m$个新的数据集，通过在$D$中进行$n$次有放回的采样方法，因此我的$m$个数据集里，每个里面都有数目相同的样本$n$个。之后就和上面的分析一样了，我就在每一个新的数据集上训练它$m$个预测器。

注意：往往数据集这种情况下，并非满足$i.i.d$，因此不可能得到方差降为$1/m$ 倍这么多。

加入训练的预测器有方差$\sigma^2$和相关系数$p$，那么我们最后计算的结果是：

上面的公式咋来的，我还没明白，懂的人麻烦给我说说。

但是总的来说，在算法中引入额外的可变性是有利的，只要它降低了样本之间的相关性。

随机森林

随机森林的公式为：

也就是说随机森林不是别的，就是加入了bagging思想的一堆决策树的联合体，在实际操作的时候，当选择决策树的每一个节点时，选择大小为 $d$ 的输入特征的一个随机子集，然后只考虑在这些子集特征上做分割；

囧：他评价随机森林可能是最好的黑盒子机器学习算法，因为它们通常在没有任何调优的情况下工作得很好。

贝叶斯最优理论（Bayes Optimality）

该理论想告诉我们一件事，不管你是什么分类器，你的性能上限永远是它，称为贝叶斯最优。

上面的分析里假设给定了测试点$X$，那么我的对应值$t$是固定的，但是现实是$t$也不是固定的，它作为$X$的条件概率为$p(t|X)$。

现在我们的预测值是一个分布的情况，那么可以测量它的期望是什么。设 $y_{\ast} = \mathbb E[t|X]$，下面的公式为在给定$X$ 的条件下，训练结果$y$与真实结果$t$的期望损失，其中后面的计算省掉了符号$\text{argmin}_y\mathbb E[(y-t)^2]$ 里的$\text{argmin}_y$:

可以看到公式最后一行的左边是非负的， 当我们的预测器学习得到分类结果 $y_{\ast}$时，第一项为0；而第二项是和$y$无关的，也就是和我们学习的$y$居然无关；对它的解释是这是targets天生带有的不确定性，或不可预知性（unpredictability）或噪声，称为贝叶斯误差(Bayes error)。

分类算法学习得到$y_{\ast}$就了不得了，称为贝叶斯最优（Bayes optimal），这也是最好的预测，因为它将预期损失最小化。

再一次对期望损失做分解，但是这次视$t$为随机变量：

对比 $t$ 不是变量的期望损失：

可以看到方差项未变，期望项里的 $t$ 成了假设的最优预测值$y_{\ast}$ ,然后便是贝叶斯误差。

Boosting

  • Boosting：按序训练分类器，每次集中训练之前分类错误的数据点

Commonsense：

加权的训练集：误分类率（损失函数）$\sum_{n = 1}^N[h(x^{(N)}) \ne t^{(n)}]$在一开始对每一个训练样本是相等的；但之后样本被误分类的权重改变了，被误分为错误类的样本带来cost，因此考虑对这部分样本做加权处理，使得分类器更关注之前被错误分类的样本，损失函数成为：

弱学习器（weak Learner）：性能稍微好于随机猜测的学习算法，所以对于加权训练集，得到的误差略小于0.5：

关注它的原因更多是因为有很高的计算效率，比如决策树，或决策树桩（decision stump），即只有一个分割的决策树。

AdaBoost(自适应提升)

  • AdaBoost的关键步骤:
    • 一、每轮迭代重新分配训练样本的权重，使得分类不正确的样本权重更大；
    • 二、在新权重样本上训练弱分类器；
    • 三、把所有的弱分类器集成为新分类器；
    • 四、重复该过程很多次；
  • 实际上弱学习器将加权误差最小化，因此AdaBoost使每个分类器更关注上一次的错误分类，从而降低了bias.

AdaBoost算法如下：

  • Input：

    • 数据集$D_N={(x^{(n)}, t^{(n)})},n=1,2,…,N$ 。
    • 弱分类器 $\text{WeakLearn}$，迭代次数$T$。

  • Output：分类器$H(x)$。

  • Initialize：采样权重$\mathbf w^{(n)} = \frac{1}{N},n =1 ,2,3…,N$。

  • For $t= 1,….,T$

    • 用$\mathbf w^{(n)}$的权重化样本训练一个弱分类器：

    • 计算权重误差（weighted error）：

    • 计算分类器系数（classifier coefficient）：

    • 更新数据集的权重：

  • Return：