LeetCode-Weekly Contest 154

Posted on Edited on In Views:

Weekly Contest 154

1189. Maximum Number of Balloons

Given a string text, you want to use the characters of text to form as many instances of the word “balloon” as possible.

You can use each character in text at most once. Return the maximum number of instances that can be formed.

1
2
>Input: text = "nlaebolko"
>Output: 1
1
2
>Input: text = "loonbalxballpoon"
>Output: 2
1
2
>Input: text = "leetcode"
>Output: 0
  • 解析：查看这个里面有多少个”ballon”单词，不能使用以及用过的字母。我用的map来做：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    int maxNumberOfBalloons(string text) {
        unordered_map<char, int> table;
        string s = "balloon";
        for (auto c : text)
        {
            if (s.find(c) != string::npos)
                table[c]++;
        }
        bool zero = true;
        int res = 0;
        while(zero)
        {
            for (auto c : s)
            {
                if(table[c] == 0) //没有c这个字符，那么不能组成单词，返回0
                    return res;
                else
                {
                    table[c]--;
                    if (table[c] == 0)//该类单词用完了，不可能再组成单词，退出循环。
                        zero = false;
                }
            }
            res += 1;//每次循环结束说明能组成一个单词。
        }
        return res;
    }
};

别人的方法：思路一样，找最小出现字符的数目就行。

1
2
3
4
5
6
7
8
class Solution:
    def maxNumberOfBalloons(self, text: str) -> int:
        ans=len(text)
        for l in 'ban':
            ans=min(ans,text.count(l))
        for l in 'lo':
            ans=min(ans,text.count(l)//2)
        return ans

1190. Reverse Substrings Between Each Pair of Parentheses

You are given a string s that consists of lower case English letters and brackets.

Reverse the strings in each pair of matching parentheses, starting from the innermost one.

Your result should not contain any brackets.

1
2
>Input: s = "a(bcdefghijkl(mno)p)q"
>Output: "apmnolkjihgfedcbq"

  • 解析：我用的python自带的find、rfind函数来做的,就是找到左右括号，然后切片反正：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    class Solution:
        def reverseParentheses(self, s: str) -> str:
            while 1:
                l = s.rfind('(')
                r = s[l:].find(')') + l
                if l == -1 or r == -1:
                    break
                s = s[:l] + s[l + 1 : r][::-1] + s[r + 1:]     
            return s

    别人的做法：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    class Solution {
    public:
        string reverseParentheses(string s) {
            int n = s.size();

            if (s.find('(') == string::npos)
                return s;

            int position = s.find('(');
            int level = 0; //记录对称的括号是否平衡

            for (int i = position; i < n; i++)
                if (s[i] == '(')
                    level++;
                else if (s[i] == ')') {
                    level--;

                    if (level == 0) {
                        string answer = s.substr(0, position);//不需要反转的左括号前的子串
                        string sub = s.substr(position + 1, i - (position + 1));//最外层括号的子串
                        sub = reverseParentheses(sub); //对内部的括号层做反转的结果
                        reverse(sub.begin(), sub.end()); //最后对最外层做反转
                        answer += sub; //加上前后的子串
                        answer += reverseParentheses(s.substr(i + 1));
                        return answer;
                    }
                }

            assert(false);
        }
    };

1191. K-Concatenation Maximum Sum

Given an integer array arr and an integer k, modify the array by repeating it k times.

For example, if arr = [1, 2] and k = 3then the modified array will be [1, 2, 1, 2, 1, 2].

Return the maximum sub-array sum in the modified array. Note that the length of the sub-array can be 0 and its sum in that case is 0.

As the answer can be very large, return the answer modulo 10^9 + 7.

若整个数组的和都小于等于0，那么k大于1时，只考虑数组的前缀和数组的后缀大小和，与数组的最大子数组和的大小，谁更大。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public:
    int kConcatenationMaxSum(vector<int>& arr, int k) {
        int mod = 1e9 + 7;
        // lmax:record maximum begin at left; 
        //rmax: record maximum begin at right;
        //mmax: record Largest Sum Contiguous Subarray: https://www.geeksforgeeks.org/largest-sum-contiguous-subarray/
        long lmax = INT_MIN, rmax =INT_MIN, mmax = INT_MIN;
        long lend = 0, rend = 0, mend = 0;
        for (int i = 0, j = arr.size() -1; i < arr.size() && j >=0; i++, j--)
        {
            lend += arr[i]; lmax = max(lmax, lend);
            rend += arr[j]; rmax = max(rmax, rend);
            mend += arr[i]; 
            if (mend < 0)
                mend = 0;
            else
                mmax =  max(mmax, mend);
        }
        if (k == 1)
            return max(long(0), mmax);
        //lend is also the sum of total array.
        //when little than 0, just compare 2 combined array.
        else if (lend <= 0) 
        {
            return max(long(0), max(lmax + rmax, mmax)) % mod;
        }
        //else plus the middle
        else 
        {
            return max(long(0), max((lend * (k - 2) + lmax + rmax), mmax)) % mod;
        }
    }
};

1192. Critical Connections in a Network

There are n servers numbered from 0 to n-1 connected by undirected server-to-server connections forming a network where connections[i] = [a, b] represents a connection between servers a and b. Any server can reach any other server directly or indirectly through the network.

A critical connection is a connection that, if removed, will make some server unable to reach some other server.

Return all critical connections in the network in any order.

Constraints:

  • 1 <= n <= 10^5
  • n-1 <= connections.length <= 10^5
  • connections[i][0] != connections[i][1]
  • There are no repeated connections.

1
2
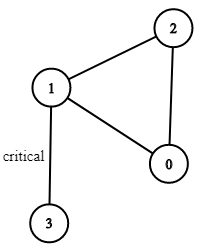
3
Input: n = 4, connections = [[0,1],[1,2],[2,0],[1,3]]
Output: [[1,3]]
Explanation: [[3,1]] is also accepted.

  • 设数组first,长度为节点的数目，first 数组来存储每个顶点其中一条边的编号。

    比如1号顶点有一条边是 “1 4 9”（该条边的编号是 1），那么就将 first[1]的值设为 1。如果某个顶点 i 没有以该顶点为起始点的边，则将 first[ i ] 的值设为-1。

  • 设数组next，长度为边的数目，next[i]存储的是“编号为i的边”的“前一条边”的编号。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    int main()
    {
        int n = 4 ,m = 5;//点数和边数
        //u、v代表一对有向边
        int u[6] = {0, 1, 4, 1, 2, 1}; //起点
        int v[6] = {0, 4, 3, 2, 4, 3}; //终点
        int i;
        int first[n + 1],next[m + 1]; //0位置处不用
        for(int i=1; i<=n; i++)
            first[i]=-1;
        for(i=1; i<=m; i++)
        {
            //当前输入第i条边;对应节点(起点)号码为u[i]
            next[i] = first[u[i]]; 
            first[u[i]] = i; 
        }
        //遍历1号顶点所有边
        int k = first[1]; //1号顶点其中的一条边的编号（其实也是最后读入的边）
        while(k != -1)
        {
            cout << u[k] << "--->" << v[k] << endl;
            k = next[k];
        }
    }

    output:
    1--->3
    1--->2
    1--->4

无向图的类似存储方式：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
    //因为是无向图，所以边的数目是 MAXM * 2.
    //Head[i]存储第i个节点的其中一条边的编号，等价于上边的first数组，next数组等价于上面的next数组
	int Head[MAXN], Next[MAXM*2], To[MAXM*2]; 
	void add_edge(int x, int y)
    {
        tot++;  //tot是输入的每条边被存储在Next和To中的索引;
        Next[tot] = Head[x];
        Head[x] = tot;
        To[tot] = y;
    }
    void ReadInfo(int n, vector< vector<int>>& connections) //n为节点数，边集如： [[0,1],[1,2],[2,0],[1,3]]
    {
        memset(Head, -1, sizeof(Head));
        tot = 0;
        for (auto &v: conn)
        {
            int x = v[0];
            int y = v[1];
            add_edge(x, y);
            add_edge(y, x);
        }
    }
//遍历顶点u的全部边
for (int i = Head[u]; i != -1; i = Next[i])
  • 类似于Tarjan 算法：Tarjan 思想：对于一个连通图，递归可以访问到所有顶点和边。
1
2
3
4
5
6
7
8
9
 ------------
|            |
1 --- 2 ---- 3
      |
	  |
      |
	  4 --- 5
	  |     |
       ---- 6

而对于割边，例如2-4，递归的时候，2-4递归的所有顶点都大于2。
而对于非割边，比如5-6，递归的时候，6可以找到更小的4。

总结一下就是，这个边递归找的最小编号都比自己大，那这个边就是割边，否则不是割边。

所以我们需要做的就是递归寻找每个顶点能够到达的最小编号，然后比大小即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void Tarjan(int v, int pre = -1)
{
    if (dfs[v] != -1) return; //已经遍历过该节点
    dfs[v] = low[v] = ++numIndex; //分配唯一编号
    
    //遍历所有顶点v出发的边
    for(int i = Head[v]; i != -1; i = Next[i])
    {
        int u = To[i]; //u:第i条边对应的终点
        if (u == pre) continue; //因为是无向图，该终点u是上次的起点则忽略该终点
        Tarjan(u, v); //递归
        
        low[v] = min(low[v], low[u]); //如有更小的编号，更新
        if (low[u] > dfs[v]) //找到一个答案
        {
            cutEdge[numCutedge++] = {v, u};
        }
    }
}

完整代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
const int MAXN = 1e5 + 10;
const int MAXE = 1e5 + 10;
class Solution {
    //Head:存储每一个节点出发的其中一条边, Next:存储每条边的上一条边,To:每条边的结尾节点位置
    int Head[MAXN], Next[MAXE * 2], To[MAXE * 2];
    
    //to:更新边的编号
    int to;
    
    //numCutedge:记录关键边的数目，numIndex:为搜索的节点分配唯一的编号
    int numCutedge, numIndex;
    
    //dfs:存储每一个节点的唯一编号; low:存储当前节点能到达的最小编号
    int dfs[MAXN], low[MAXN];
    
    struct edge
    {
        int u, v;
    }cutEdge[MAXE];
    
    void Tarjan(int v, int pre = -1)
    {
        if (dfs[v] != -1) return; //已经遍历过该节点
        dfs[v] = low[v] = ++numIndex; //分配唯一编号
        
        //遍历所有顶点v出发的边
        for(int i = Head[v]; i != -1; i = Next[i])
        {
            int u = To[i]; //u:第i条边对应的终点
            if (u == pre) continue; //因为是无向图，该终点u是上次的起点则忽略该终点
            Tarjan(u, v); //递归
            
            low[v] = min(low[v], low[u]); //如有更小的编号，更新
            if (low[u] > dfs[v]) //找到一个答案
            {
                cutEdge[numCutedge++] = {v, u};
            }
        }
    }
    
    void solve()
    {
        numCutedge = 0, numIndex = 0;
        memset(dfs, -1, sizeof(dfs));
        memset(low, -1, sizeof(low));
        Tarjan(0); //由于是连通图，随便找个定点开始搜就行了
    }
    
    void outit(vector<vector<int>> &ans)
    {
        for (int i = 0; i < numCutedge; i++)
        {
            ans.push_back({cutEdge[i].u, cutEdge[i].v});
        }
    }
    
    void add_edge(int x, int y)
    {
        to++;
        Next[to] = Head[x]; //next[i]存储的是“编号为i的边”的“前一条边”的编号
        Head[x] = to; //储存to这条边
        To[to] = y;
    }
    
    void readInfo(int n, vector< vector<int>>& cons)
    {
        memset(Head, -1, sizeof(Head));
        // this->n = n;
        to = 0;
        for (auto &e: cons)
        {
            int x = e[0];
            int y = e[1];
            add_edge(x, y);
            add_edge(y, x);
        }
    }
    
public:
    vector<vector<int>> criticalConnections(int n, vector<vector<int>>& connections) {
        readInfo(n, connections);
        solve();
        vector< vector<int>> ans;
        outit(ans);
        return ans;
    }
};

python:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
import collections
class Solution:
    def criticalConnections(self, n: int, connections: List[List[int]]) -> List[List[int]]:
        def make_graph(cons):
            graph = collections.defaultdict(list)
            for i, j in cons:
                graph[i].append(j)
                graph[j].append(i)
            return graph
        
        graph = make_graph(connections)
        connections = set(map(tuple, (map(sorted, connections))))
        rank = [-2] * n
        def dfs(node, depth):
            if rank[node] >= 0:
                # visiting (0<=rank<n), or visited (rank=n)
                return rank[node]
            rank[node] = depth #设置为深度值
            
            min_depth = n 
            for neiborhood in graph[node]:
                if rank[neiborhood] == depth - 1: #无向图回到上一步访问点
                    continue 
                back_depth = dfs(neiborhood, depth + 1)
                
                if back_depth <= depth:
                    connections.discard(tuple(sorted((node, neiborhood))))
                min_depth = min(min_depth, back_depth) # 能返回更小的深度说明循环回去有环
            rank[node] = n #又重新设置回来 - -
            return min_depth
        dfs(0, 0)
        return connections