GAN

原始GAN

训练过程：

1. 初始化generator和discriminator
2. 在每一轮迭代中：
   • 首先固定生成器 $G$，然后更新判别器$D$；这时候，$D$学会对真实目标打高分，生成目标打低分；
   • 固定判别器$D$，然后更新生成器$G$；这时候，生成器（通过梯度上升）学习如何欺骗判别器；

训练过程公式版：

1. Initialize：初始化$D: \theta_d$，$G:\theta_g$；

2. Each Iteration：

   • Learning $D$ ：1. 采样$m$个实例样本；2. 采样$m$个噪声样本$z^{(1…i)}$；3. 得到生成数据$\tilde x^i = G(z^i)$；4. 更新判别器$D$的参数来最大化： $$\tilde V = \frac{1}{m}\sum_{i=1}^m\log D(x^i) + \frac{1}{m}\sum_{i=1}^m\log (1 - D(\tilde x^i)) \\\\ \theta_d \leftarrow \theta_d + \eta \nabla \tilde V(\theta_d)$$

• Learning $G$ ：1.采样$m$个噪声样本；2.更新生成器参数$\theta_g$ 来最大化： $$\tilde V = \frac{1}{m} \sum_{i=1}^m \log (D(G(z^i))) \\\\ \theta_g \leftarrow \theta_g - \eta\nabla \tilde V(\theta_g)$$

Structured Learning

含义：机器学习是找到一个函数$f:X \rightarrow Y$，回归输出一个标量，分类输出一个类别，而结构化学习输出一个序列，一个矩阵，一个图或树等，这些输出由具有依赖性的组件（component）组成。

带来的学习挑战：机器学习算法需要学会做规划（planning），因为输出组件之间具有依赖性，所以应该全局地去考虑生成它们。

从这个角度去分析的话，生成器像自底向上的方式，学习在组件级别上生成目标；判别器像自顶向下的方式，学习评价全部的对象，找到最好的那一个。

生成器$G$：是一个神经网络，它定义了一个分布$PG(x)$，分布中的数据由此组成$x=G(z)$；为了拟合真实数据分布$P{data}$,我们可以写：

$$G^{\ast} = \arg\min_G \mathrm{Div}(P_G,P_{data})$$

虽然不知道分布$PG(x)$还有$P{data}$，但是我们可以从中采样来近似它们。上面的目标函数与训练线性回归二分类器完全相同。

判别器$D$：目标函数如下，但是$G$已经固定：

$$V(G,D) = E_{x\sim P_{data}}[\log D(x)] + E_{x\sim P_G}[\log (1 - D(x))]$$

训练$D$，当散度越小，越难判断出真伪：

$$D^{\ast} =\arg \max_D V(D, G)$$

• 生成器的优点：即使使用深度模型也很容易生成
• 生成器的缺点：组件之间的相关性很难学习；模仿的是外观；
• 判别器的优点：从大局考虑
• 判别器的缺点：生成并不总是可行的，尤其是当您的模型很深入时；如何生成比较真的负样本，因为过于假的样本通常得分很低；

Conditional GAN

原始GAN：输入：条件$c$还有噪声$Z$，得到伪造图片$x=G(c,z)$，$x$作为判别器$D$的输入得到该$x$是真假的一个判断值，但看到上面的这个过程没有利用输入的条件$c$。

条件GAN：不同在于输入判别器$D$的为：条件$c$还有$x$，判断$x$是否为真 + 判断$c$还有$x$是否匹配。比如输入判别器的为（文本：”火车”，图像： 火车的照片）。有的其他论文也通过把$x$输入$D$，然后把$D$的输出与条件$c$作为另一个神经网络的输入，两个网络输出同时来做判断。

Stack GAN

17年的ICCV工作，输入一段文本向量，它朝着两个网络输入：第一个：在第一层通过条件增强（CA：conditional augmentation）后输入生成器$G_1$做摘要（sketch），上游采样（upsampling）后得到伪造图片，然后输出判别器$D_1$。第二个：输入生成器$G_2$做提纯（refinement）,上游采样后得到伪造图片，结合真实图片输入到判别器$D_2$.

Patch GAN

对图片的一个小局部做生成对抗。

Unsupervised Conditional Generation

使用特点：在没有成对数据的情况下将对象从一个域转换到另一个域，如style transfer。

李老师介绍了很多论文中GAN的设计结构，下面记录下。

这通常有两种方法：

1. 第一类方法：直接从定义域$X$到$Y$的迁移$G_{X\rightarrow Y}$；

2. 第二类方法：编码的方法，去投影到隐层只保留语义信息,$X\rightarrow \mathrm{Encoder}_X\rightarrow \mathrm{AttributeLayer}\rightarrow \mathrm{Decoder}_Y \rightarrow Y$

第一类方法：

最早的直接做法：把$X$直接输入$G_{X\rightarrow Y}$里产生一个类似的$\hat Y$，结合一个真正来自$Y$域的输入，一起放到判别器$D_Y$做训练。

缺点：$\hat Y$ 完全把$X$的特征消除了，太过于类似$Y$了。

发现简单的生成器$G$更容易保持原来的域特性，而根本的解决办法是新的GAN架构，比如CycleGAN，多域迁移的starGAN。

Cycle GAN

结构是$X\rightarrow G{X \rightarrow Y} \rightarrow \hat Y \rightarrow G{Y\rightarrow X} \rightarrow \hat X$，然后重构损失 ：$L=\mathrm{(\hat X，X)}$。

同时$\hat Y$ 会输入判别器$D_Y$ ；

同时对于域$Y$的样本，有$Y\rightarrow G{Y \rightarrow X} \rightarrow \hat X \rightarrow G{X\rightarrow Y} \rightarrow \hat Y$，然后重构损失 ：$L=\mathrm{(\hat Y，Y)}$。

同时$\hat X$会输入判别器$D_X$；

总的来看，从开始到结束，是遵从所谓的周期一致性（Cycle Consisitency）。

第二类方法：

基本上是编码器的使用，如双层编码器，输入$X1$经过上层编码器$\mathrm{Encoder}_X$编码后会放到下一层解码器$\mathrm{Decoder}_Y$，然后输出结果在输入下层判别器$D{Y}$。

GAN Theory

给定一个数据分布$P{data}(x)$（可以从里面采样），设一个带参分布$P_G(x;\theta)$，目的是为了找到$\theta$使得$P_G(x;\theta)\approx P{data}(x)$ ；比如可以假设$P_G(X;\theta)$是一个混合高斯分布。

推理的flow是这样的：先从$P_{data}(x)$中采样${x^1,x^2,…,x^m}$，由此计算$P_G(x^i;\theta)$，生成样本的似然函数为：

$$L(\theta) =\prod_{i=1}^nP_{G}(x^i;\theta)$$

最大化似然函数来找寻$\theta^{\ast}$：

$$\begin{align*} \theta^{\ast} &= \arg\max_{\theta}\prod_{i=1}^mP_G(x^i;\theta) =\arg\max_{\theta} \log\prod_{i=1}^mP_G(x^i;\theta) \\\\ & =\arg\max_{\theta} \sum_{i=1}^m\log P_G(x^i;\theta) \\\\ & \approx \arg\max_{\theta} E_{x\sim P_{data}}[\log P_{G}(x;\theta)] \\\\ &= \arg\max_{\theta} \int_{x}P_{data}(x) \log P_{G}(x;\theta)\mathrm{dx} -\int_{x}P_{data}(x)\log P_{data}(x)\mathrm{dx} \\\\ &= \arg \min_{\theta} KL(P_{data} \Vert P_G) \end{align*}$$

生成器$G$用神经网络来定义概率分布$P_G$，最优的$G^{\ast}$目标函数是：

$$\arg \min _G \mathrm{Div}(P_G,P_{data})$$

怎么计算这个散度？

虽然不知道$PG$与$P{data}$，但是可以先从这里面采样，其中$P{data}$采集于训练样本，$P{G}$采集于正态分布，

这些样本输入到判别器$D$，用sigmoid函数对输出做二分类，目标函数是一个二分类损失函数（binary cross-entropy），其中$G$已经固定了：

$$V(G,D) = E_{x \sim P_{data}}[\log D(x)] + E_{x\sim P_G}[\log (1- D(x))]$$

• 给定了$G$,也就有了负样本，这时候训练判别器$\max_{D}V(G, D)$

$$\begin{align*} V &= E_{x\sim P_{data}}[\log D(x)] + E_{x \sim P_G}[\log (1-D(x))] \\\\ &= \int_{x}P_{data}(x)\log D(x) \mathrm{dx} + \int_xP_G(x)\log(1-D(x))\mathrm{dx} \\\\ &= \int_x \big[P_{data}(x)\log D(x) + P_G(x) \log (1-D(x))\big] \mathrm{dx} \end{align*}$$

因此可以看出来,给了$x$，最后的$D^{\ast}$最大化$f(D)$：

$$f(D) = P_{data}(x)\log D(x) + P_G(x) \log (1-D(x))$$

求导得到如下：

$$D^{\ast}(x) = \frac{P_{data}(x)}{P_{data}(x) +P_G(x)}$$

把这个公式带入原来的$V(G, D)$得到：

$$\begin{align*} &\max_{D}V(G,D) \\\\ &= V(G, D^{\ast}) \\\\ &= E_{x\sim P_{data}}\bigg[\log \frac{P_{data}(x)}{P_{data}(x) +P_G(x)} \bigg] + E_{x \sim P_{G}}\bigg[\log \frac{P_{G}(x)}{P_{data}(x) +P_G(x)} \bigg] \\\\ &=-2\log 2 + \int_x P_{data}(x)\bigg[\log \frac{P_{data}(x)}{(P_{data}(x) +P_G(x))/2} \bigg] + \int _xP_{G}(x)\bigg[\log \frac{P_{G}(x)}{(P_{data}(x) +P_G(x))/2} \bigg] \\\\ &=-2\log2 + \mathrm{KL}(P_{data}(x) \Vert \frac{P_{data}(x) +P_G(x)}{2}) + \mathrm{KL}(P_{G}(x) \Vert \frac{P_{data}(x) +P_G(x)}{2}) \\\\ &=-2\log 2 + 2\mathrm{JSD}(P_{data}\Vert P_G) \end{align*}$$

其中用的的$JS$散度公式为：

$$\mathrm{JSD}(P\Vert Q) = \frac{1}{2}D(P \Vert M) + \frac{1}{2}D(Q \Vert M) \\\\ M = \frac{1}{2}(P+Q)$$

更新完了一轮判别器，开始更新生成器的参数 ：

$$G^{\ast}=\arg \min_{G}\max_DV(G,D)$$

其中判别器部分可以视为关于$G$的函数： $L(G)=\max_DV(G,D)$，由此得到训练GAN的过程如下：

最小化损失函数$L(G)$，其中这里的$L(G)$是带有$\max$ 运算符号的，它的每次求解都是把对应最大函数值的函数段拿来做损失更新计算：

$$\theta_G \longleftarrow \theta_G -\eta\partial L(G)/\partial \theta_G$$

• 给定初始的$G0$，找到$D_0^{\ast}$，梯度上升最大化$V(G_0,D)$：得到$V(G_0,D_0^{\ast})$是$P{data}(x)$与$P_{G_0}(x)$的JS散度；
• 利用$\thetaG \longleftarrow \theta_G -\eta\partial V(G_0,D_0^{\ast})/\partial \theta_G$ 得到$G_1$；存在的问题是当更新为$G_1$后，$V(G_1,D_0^{\ast})$ 函数下的$D^{\ast}$已经不再是$P{data}(x)$与$P_{G_0}(x)$的JS散度，由下图可知：

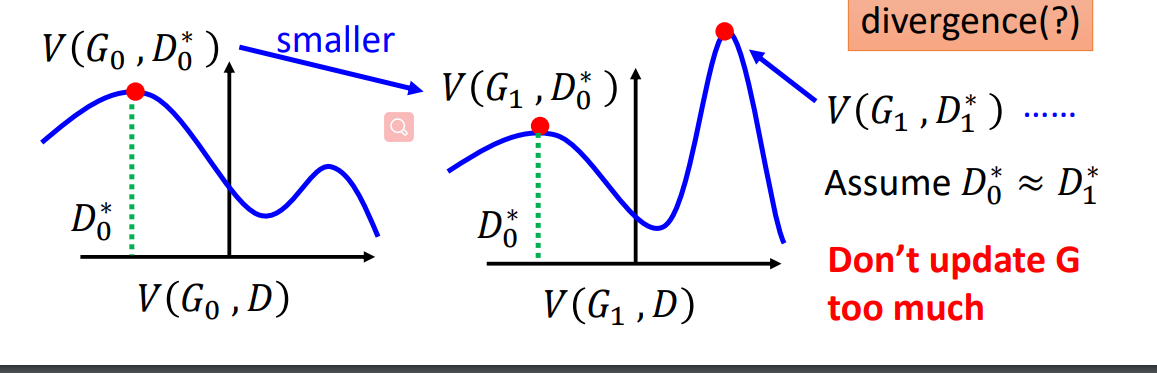
训练$D$要求的是最小化JS散度，当更新为$G_1$后，它的JS散度位置变了，此时再做更新$D_1^{\ast}$若想在上一轮的JS散度处，那么必须假设$D_0^{\ast}=D_1^{\ast}$，换句话说，要先训练判别器$D$多次，再去训练$G$.

下面是整个算法流程图：

在实际使用的论文代码中，不是用的$V=E{x\sim P{G}}[\log (1-D(x))]$更新生成器，而是用$V=E{x\sim P{G}}[-\log (D(x))]$来更新生成器，此时把来源于$P_G$的标签$x$作为正样本便可。

Tips for Improving GAN

结论是原始GAN的JS散度并不适用，因为真实数据分布，比如图片的分布，实际上是高维空间中的一个低维manifold，因此对整个高维空间中的两个分布$P{G}$还有$P{data}$ ，它们一开始就很大可能一点都不重合（overlap），就算它们会有部分的重合，但实际我们是sampling的方式来近似$P{G}$还有$P{data}$ 的，我们的采样数目也使得我们得不到它们的重合。

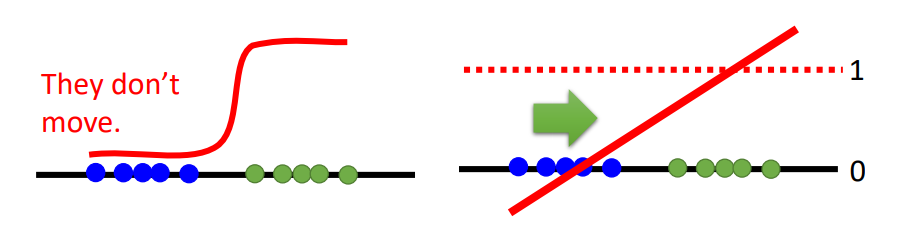
造成的结果就是我们的JS度量一直是$\log 2$，也就是一个常数，也就是如果两个分布不重叠，二分类器可以达到100%的准确率。如下图，这样的话，对于sigmoid函数，蓝色点为生成样本，我们想要的是它沿着sigmoid函数变成绿色训练数据样本点，但是因为它一直被完全判断为负样本，它的更新梯度几乎没有，所以达不到我们想要的效果。

对此有人提出LSGAN(Least Square GAN)：把sigmoid分类函数去掉，用线性回归取代。

WGAN

这是一个更好的对GAN的改进方法，它用的是Earth Mover Distance来度量数据分布$P{data}$还有$P{G}$之间的距离。

Earth Mover’s Distance

把分布$P$推成分布$Q$的最小平均距离就是推土机距离，其中有很多推土方案(moving plan),记为$\gamma$,推土方案是可以用一个矩阵表示如下，矩阵中每个元素表示有多少土从$P$移动到$Q$，移动的越多的位置颜色越亮：

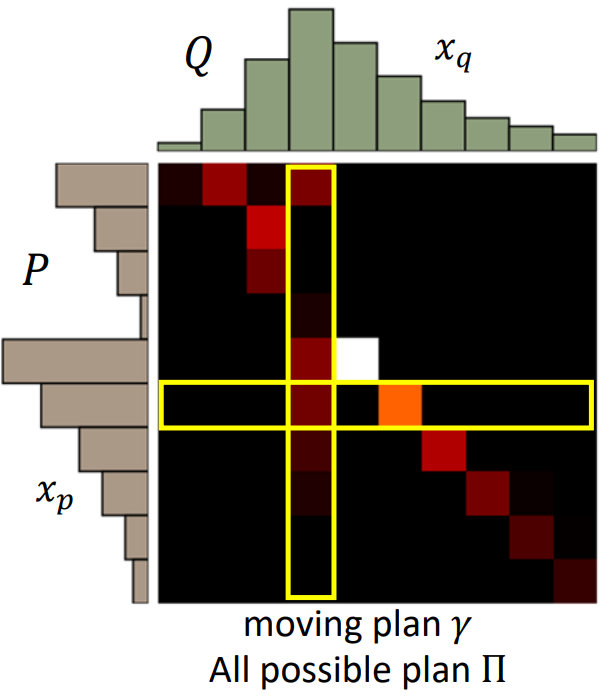
其中一个方案$\gamma$的平均距离为：

$$B(\gamma) = \sum_{x_p, x_q} =\gamma(x_p, x_q)\Vert x_p - x_q \Vert$$

推土机距离是最下移动距离（最优）方案：

$$W(P,Q) =\min_{\gamma\in \prod} B(\gamma)$$

该wasserstein distance之所以比JS好，是因为$P{G}$与$P{data}$即使没有overlap，我也可以从这个距离看到，它们之间的差异是在降低的，但是对JS的话，可能就会一直是一个常数。

具体添加W距离到GAN的目标函数里：

$$V(G,D) = \max_{D\in \mathrm{1-Lipschitz}}\big\{E_{x\sim P_{data}}[D(x)] -E_{x\sim P_{G}}[D(x)] \big \}$$

上面的$\mathrm{1-Lipschitz}$是在说$D$必须是足够smooth的，否则，训练$D$的时候不会拟合，上面的左边会趋向无穷，右边会趋向负无穷。

Lipschitz函数的定义是：

$$\Vert f(x_1) -f(x_2) \Vert \le K \Vert x_1 -x_2\Vert$$

当$K=1$时，上式为$\mathrm{1-Lipschitz}$函数，左边代表的是输出的改变，右边代表的是输入的改变，$\mathrm{1-Lipschitz}$的意思是输出的改变不能太快，应该是不大于输入的改变。

weight clipping

但是这个约束并不好实现，当时的方案称为权重剪裁：强制$D$的权重$W$范围为$|W|<c$便可以了，但是这个并不保证上面的约束成立。

Improved WGAN (WGAN-GP)

A differentiable function is 1-Lipschitz if and only if it has gradients with norm less than or equal to 1 everywhere.

也就是下面的式子等价：

$$D\in \mathrm{1-Lipschitz} \iff \Vert \nabla_xD(x) \Vert \le 1 ,\text{for all x}$$

通过在训练$D$的时候添加一个惩罚因子达到这一点：

$$V(G, D) \max_D\big\{E_{x\sim P_{data}}[D(x)] - E_{x\sim P_G}[D(x)] - \\\\ \lambda E_x\sim P_{penalty}[\max(0,\Vert \nabla_xD(x)\Vert-1)]\big\}$$

其中得到分布$P{penalty}$的方式是从$P{data}$与$P{G}$中采样，然后在它们连线上作为分布$P{penalty}$，为什么这样做的原因是：

Given that enforcing the Lipschitz constraint everywhere is intractable, enforcing it only along these straight lines seems sufficient and experimentally results in good performance

而实现的时候采用的是：$(\Vert \nabla_xD(x)\Vert-1)^2$，也就是使得梯度值小于大于1都会有惩罚，而上面的只对大于1的梯度做惩罚。

WGAN的算法流程如下：

此外还有Spectrum Norm方法。

Spectral Normalization → Keep gradient norm smaller than 1 everywhere。

Energy-based GAN (EBGAN)：替换了判别器$D$的架构，换成了autoencoder。利用自动编码器的负构误差来确定图片的好坏，好处是判别器可以先做预训练。此方法对判别来时$G$的图片不会给出太大的负值。

Loss-sensitive GAN (LSGAN)，每次计算$G$更新的好坏程度。