斐波那契递归: 由斐波那契数列的递归关系推导出n>2时的状态矩阵,然后利用快速矩阵乘法完成;
知识点:
$n^m$次方,等于计算$n^{2^{(10010101..1101)}}$,用$m$的二进制位完成乘法;
幂计算的过程中,有$m\&1$判断$m$的最右一个bit位是否为1;
1 | //1. |
同类型的题:青蛙跳台阶,一次能跳1或者2步,求跳到n个台阶可能的跳法。
1.最后的状态矩阵为$(F(n),F(n-1))=(F(n-1),F(n-2))* \begin{bmatrix}1 & 1\1 & 0\end{bmatrix}=\cdots=(2,1)\times\begin{bmatrix}1 & 1\1 & 0\end{bmatrix}^{n-2}$
1 |
|
假设农场中成熟的母牛每年只会生 1 头小母牛,并且永远不会死。第一年农场中有一只成熟的母牛,从第二年开始,母牛开始生小母牛。每只小母牛 3 年之后成熟又可以生小母牛。给定整数 n,求出 n 年后牛的数量。
- 类似一样是求解状态矩阵:设
1 |
|
题目描述:给定一个 n * m 的矩阵 a,从左上角开始每次只能向右或者向下走,最后到达右下角的位置,路径上所有的数字累加起来就是路径和,输出所有的路径中最小的路径和。
解析:动态规划:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
using namespace std;
int minPathSum1(const vector<vector<int>> &mat)
{
if(mat.empty()) return 0;
int row = mat.size(), col = mat[0].size();
if(row ==0 || col==0) return 0;
vector<vector<int>> table(row, vector<int>(col, 0));
table[0][0] = mat[0][0];
for(int i=1; i<col;++i)
table[0][i] = mat[0][i] + table[0][i-1]; //tag:easy error
for(int j=1; j<row; ++j)
table[j][0] = mat[j][0] + table[j-1][0]; //tag:easy error
for(int i=1; i<row; ++i)
{
for(int j=1; j<col; ++j)
{
table[i][j] = min(table[i-1][j],table[i][j-1]) + mat[i][j];
}
}
return table[row-1][col-1];
}
int main()
{
int m, n;
cin >> m >> n;
vector<vector<int>> vec(m,vector<int>(n, 0));
for(int i=0; i<m; ++i)
{
for(int j=0;j<n; ++j)
{
cin>>vec[i][j];
}
}
int res = minPathSum1(vec);
cout << res << endl;
return 0;
}
方法2:空间复杂度降低为$O(\min(M,N))$,滚动的更新一个数组来保存结果,比如列少行多,那初始化第一行,每次滚动到下一行做更新;$arr[0]=arr[0] + \text{下一行第0列的值}$,然后对于每一列$j \rightarrow N$有$arr[j]=\min (arr[j-1],arr[j])+mat[i][j]$,也就是左边与右边的最小dp值加上当前的数组值:
1 |
|
题目描述:假设有排成一行的N个位置,记为1~N,开始时机器人在M位置,机器人可以往左或者往右走,如果机器人在1位置,那么下一步机器人只能走到2位置,如果机器人在N位置,那么下一步机器人只能走到N-1位置。规定机器人只能走k步,最终能来到P位置的方法有多少种。由于方案数可能比较大,所以答案需要对1e9+7取模。
1 | 输出包括一行四个正整数N(2<=N<=5000)、M(1<=M<=N)、K(1<=K<=5000)、P(1<=P<=N)。 |
1 | 输出一个整数,代表最终走到P的方法数对10^9+7109+7取模后的值。 |
暴力递归->动态规划->空间压缩
解析:当前处于cur位置,还剩rest步要走;1<=cur<=N
- cur==1,那么下一步只能往右走,也就是走到2,还剩rest-1步;
- cur==N,那么下一步只能往左走,也就是走到N-1,还剩rest-1步;
- cur在中间位置,可以往左(cur-1)或者右走(cur+1),还剩rest-1步,
- 终止条件:rest==0,若定在p处,返回1表示能走到,返回0表示未走到;
1 |
|
给定数组arr,arr中所有的值都为正整数且不重复。每个值代表一种面值的货币,每种面值的货币可以使用任意张,再给定一个aim,代表要找的钱数,求组成aim的最少货币数。
输出一个整数,表示组成aim的最小货币数,无解时输出-1.
- 解析:时间复杂度$O(n*aim)O(n∗aim)$,空间复杂度$O(n)O(n)$。
//dp:无后效性:前面用了x张面值为t1的钱币,用了y张面值为t2的钱币;$xt1==yt2$,此时后续的搜索是同样的结果,因此无后效性;
//cur的范围:从$0<=cur<=N$,即迭代所有的面值;total的范围:从$0<=total<=total$;
//每行是迭代的面值,每列是迭代的剩余值,面值从0取到N结束,再判断是都是有效的,也就是最后的剩余值为0,即$DP[N][0]$处;
//最终状态:有效位置$dp[N][0]$处为0,其余部分是-1;$dp[0][total]$为题目要求的结果;
1 |
|
换钱的方法数
给定数组arr,设数组长度为n,arr中所有的值都为正整数且不重复。每个值代表一种面值的货币,每种面值的货币可以使用任意张,再给定一个整数aim,代表要找的钱数,求换钱的方法数有多少种。由于方法的种数比较大,所以要求输出对10^9+7109+7进行取模后的答案.
- 解析:明确$\text{dp[N][aim]}$ 的意思:用面值为arr[1…N]的纸币,换面值为aim的钱有几种方式,最后初始第一行,每行结果只依赖于上一行左边1位与当前行左边的$\text{ [j-arr[i]]}$ 处。
1 |
|
打气球的最大分数
给定一个数组arr,长度为n。代表排有分数的气球。 每打爆一个气球都能获得分数,假设打爆气球的分数为X,获得分数的规则如下:
1)如果被打爆气球的左边有没被打爆的气球,找到离被打爆气球最近的气球,假设分数为L:如果被打爆气球的右边有没被打爆的气球,找到离被打爆气球最近的气球,假设分数为R.获得分数为LXR
2)如果被打爆的气球的左边有没被打爆的气球,找到离被打爆气球最近的气球,假设分数为L:如果被打爆气球的右边所有气球都已经被打爆,获得分数为LX。
3)如果被打爆气球的左边所有的气球都已经被打爆:如果被打爆气球的右边有没被打爆的气球,找到离被打爆气球最近的气球。获得分数为XR.
4)如果被打爆气球的左边和右边所有的气球都已经被打爆。获得分数为X。
目标是打爆所有气球,获得每次打爆的分数。通过选择打爆气球的顺序,可以得到不同的总分,请返回能获得的最大分数。
2
3
4
5
6
7
8
3
3 2 5
输出
50
2->1->3 3*2*5+3*5+5=50
解析:
设要打爆arr[L..R]范围的所有气球,并且假设arr[L-1]和arr[R+1]都没有打爆,记为process(L,R);
1.最后打爆arr[L]的方案;
2.最后打爆arr[R]的方案;
3.最后打爆arr[i]的方法,其中有 L..i…R;
去上面三种情况中最大的便是最大得分,同时记arr的开头和结尾都是1,这样便不用考虑越界问题。
1 |
|
最长递增子序列
给定数组arr,设长度为n,输出arr的最长递增子序列。(如果有多个答案,请输出其中字典序最小的)
2
3
4
5
6
7
9
2 1 5 3 6 4 8 9 7
输出
1 3 4 8 9
解析:1.动态规划算法:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
using namespace std;
/*
1. O(N^2)的解法
2. O(NlgN)的解法:利用辅助数组配合使用二分查找;
step1: 得到dp表
设dp[i]为数组arr以第i个元素结尾的时候最长递增子序列的长度;
若arr[i]结尾,那么在arr[0...i-1]中所有比arr[i]小的数都可以作为倒数第二个数;选择以结尾有最长递增子序列的数;
即dp[i] = dp[j] + 1, 其中有 0<= j < i;
step2:从dp里得到最长递增子序列
先遍历dp找到最大数的位置i,该i位置的数为递增子序列的结尾数字;
然后从右到左寻找递增子序列的倒数第2个数, 它的位置j满足dp[j] + 1 = dp[i];依次下去;
*/
vector<int> getdp1(const vector<int> &arr)
{
vector<int> dp(arr.size(), 0);
for(int i=0; i < arr.size(); ++i)
{
dp[i] = 1;
for (int j = 0; j < i; j++)
if(arr[j] < arr[i]) dp[i] = max(dp[i], dp[j] + 1);
}
return dp;
}
//辅助数组ends[i]里存着长度为i+1的递增序列结尾最小的数,如2,5 2,3则,ends[1]=3里存着长度为2的递增序列结尾最小数
vector<int> getdp2(const vector<int> &arr)
{
vector<int> dp(arr.size(), 0);
vector<int> ends(arr.size(), 0);
ends[0] = arr[0];
dp[0] = 1;
int right = 0, l = 0, r = 0 , m = 0;
for(int i = 1; i < arr.size(); i++)
{
l = 0; r = right;
while(l <= r){
m = l + (r - l)/ 2;
if (arr[i] > ends[m]) l = m + 1; //最终递归结束时排查了ends里最末的数字,l等于ends的长度
else r = m - 1;
}
right = max(right, l);
ends[l] = arr[i];
dp[i] = l + 1;
}
return dp;
}
vector<int> generateLIS(const vector<int> &arr, const vector<int> &dp)
{
int len = 0;
int index = 0;
for (int i = 0; i < dp.size(); i++)
{
if (dp[i] >= len){len = dp[i]; index = i;}
}
vector<int> LIS(len, 0);
LIS[--len] = arr[index];
for(int i = index; i >= 0; i--)
//两个条件:1.小于结尾;满足差为1;
if(dp[i] + 1 == dp[index] && arr[i] < arr[index])
{
index = i;
LIS[--len] = arr[i];
}
return LIS;
}
int main()
{
int N; cin >> N;
vector<int> arr(N, 0);
for (int i = 0; i < N; i++) cin >> arr[i];
vector<int> dp = getdp2(arr);
vector<int> LIS = generateLIS(arr, dp);
for(auto i : LIS) cout << i << " ";
}
信封嵌套问题
给n个信封的长度和宽度。如果信封A的长和宽都小于信封B,那么信封A可以放到信封B里,请求出信封最多可以嵌套多少层。
2输出包括一行,代表信封最多嵌套多少层。
解析:先按着信封的长度顺序排列好,然后对宽度的处理与最长递增子序列一样;
注:c++中的
multimap<int, int> table是按键有序的,因此放入其中已经有序。倒序的存储先设置比较的函数
multimap<int, int, greater<int>>1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
using namespace std;
int countLetter(const vector<int> &width)
{
vector<int> table;
for (int i = 0; i < width.size(); ++i)
{
auto it = lower_bound(table.begin(), table.end(), width[i]);
if (it == table.end()) table.push_back(width[i]);
else
*it = width[i];
}
return table.size();
}
int main()
{
int N; cin >> N;
multimap<int, int> table;
int a, b;
for (int i = 0; i < N; i++)
{
cin >> a >> b;
table.insert(make_pair(a, b));
}
vector<int> width;
for (auto it = table.begin(); it != table.end(); ++it)
{
width.push_back(it->second);
}
cout << countLetter(width);
}
汉诺塔问题
汉诺塔问题比较经典,这里修改一下游戏规则:现在限制不能从最左侧的塔直接移动到最右侧,也不能从最右侧直接移动到最左侧,而是必须经过中间。求当塔有n层的时候,打印最优移动过程和最优移动总步数。
2
2
3
4
5
6
7
8
9
10
11
Move 1 from left to mid
Move 1 from mid to right
Move 2 from left to mid
Move 1 from right to mid
Move 1 from mid to left
Move 2 from mid to right
Move 1 from left to mid
Move 1 from mid to right
It will move 8 steps.
2
- 解析:递归解决,因为必须经过中间,那么递归函数从左到右、从右到左,其中插入经过中间的打印函数;
1 |
|
最常公共子序列
给定两个字符串str1和str2,输出连个字符串的最长公共子序列。如过最长公共子序列为空,则输出-1。给定两个字符串str1和str2,输出连个字符串的最长公共子序列。如过最长公共子序列为空,则输出-1。
2
2
3
B1D23CA45B6A
2
解析:1. 最长公共子序列:先初始化dp的第一行和第一列,从左到右,从上到下计算每一个
dp[i][j];含义是str1[0...i]与str[0....j]的最长公共子序列的长度。 2. 回溯的过程也是判断怎么生成dp的过程,如果
dp[i][j]位置大于左边i-1和上边j-1位置,那么该i处的字符属于公共最长里的,否则网上或左走就行。
1 |
|
最长公共子串
给定两个字符串str1和str2,输出两个字符串的最长公共子串,如果最长公共子串为空,输出-1。
2
3
4
5
12345EF
输出:
2345
- 两种方法如下:
1 |
|
最小编辑代价
给定两个字符串str1和str2,再给定三个整数ic,dc和rc,分别代表插入、删除和替换一个字符的代价,请输出将str1编辑成str2的最小代价。
2
2
3
4
5
adc
5 3 2
2
- 解析如下:
1 |
|
子数组异或和为0的最多划分
给定一个整型数组arr,其中可能有正有负有零。你可以随意把整个数组切成若干个不相容的子数组,求异或和为0的子数组最多可能有多少个?整数异或和定义:把数组中所有的数异或起来得到的值。
2
2
3
4
5
3 2 1 9 0 7 0 2 1 3
Output:
4
>最优划分:{3,2,1},{9},{0},{7},{0},{2,1,3} 其中{3,2,1},{0},{0},{2,1,3}的异或和为0
- 解析如下:
1 |
|
N皇后问题
N皇后问题是指在N*N的棋盘上要摆N个皇后,要求任何两个皇后不同行,不同列也不再同一条斜线上,求给一个整数n,返回n皇后的摆法。
2
3
92
- 解析:考虑递归解法:
- 用一个等于输入N的数组来记录,其中 value of table[i] means column position of a Queen in row i.
- 注重点:(a,b)位置放置了一个皇后,那它的对角线位置(i,j)满足公式:|a-i| == |b-j|
1 |
|
1 |
|
位运算加速:
1 | 与 (and): 5 & 6 = 4 (101 & 110 = 100) |
左移n位等价于乘以$2^n$:
1 | int main() |
1 | upperLim = (1 << n) - 1 # 使得二进制表示的最右边n位都为1.其他都为0 |
- process2:返回值代表剩余的皇后在之前的皇后的影响下,有多少种合法的摆法。
- upperLim:表示当前行哪些位置可以放置皇后,1代表可以放置,0代表不能放置。八皇后问题中初始时为00000…000011111111,也就是32位整数的255。
- colLim:表示递归计算到上一行,那些列已经放置了皇后,1代表已经放置,0代表没有放置。
- leftDiaLim:表示递归计算到上一行为止,因为受以放置的所有皇后的左下方斜线的影响,导致当前行不能放置皇后,1代表不能放置,0代表可以放置。
- 表示递归计算到上一行为止,因为受以放置的所有皇后的右下方斜线的影响,导致当前行不能放置皇后,1代表不能放置,0代表可以放置。
- 变量pos:代表在当前行colLim、leftDiaLim、rightDiaLim三个状态的影响下,还有哪些位置是可选择的,1代表可以选择,0代表不能选择。
- 变量mostRightOne代表在pos下,最右边的1在什么位置。然后从右到左一次筛选出pos中可选择的位置进行递归尝试。
1 | int process2(int upperLim, int colLim, int leftDiaLim, int rightDiaLim) |
jumpGame
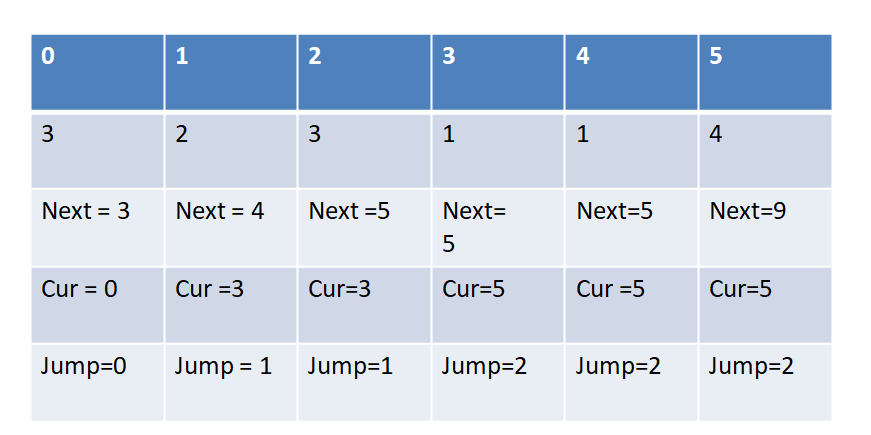
给定数组arr,arr[i]==k 代表可以从位置向右跳1~k个距离。比如,arr[2] ==3,代表可以从位置2跳到位置3、位置4或位置5。如果从位置0出发,返回最少跳几次能跳到arr最后的位置上。
2
2
解析:跳跃的是一个距离范围,因此记下每一次迭代到arr[i]后,可能跳到的最远地方就行;取最大的那个。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25int jumpGame(const vector<int> &arr)
{
int jump = 0, cur = 0, next = 0;
for (int i = 0 ; i < arr.size(); i++)
{
if (cur < i)
{
cur = next ;
jump++;
}
//记下能跳的最远距离,因为可以跳的是一个范围;
next = max(next,(i + arr[i]));
}
return jump;
}
int main ()
{
int n; cin >> n;
vector<int> arr(n, 0);
for (size_t i = 0; i < n; i++)
cin >> arr[i];
cout << jumpGame(arr) << endl;
}数组中的最长连续子序列
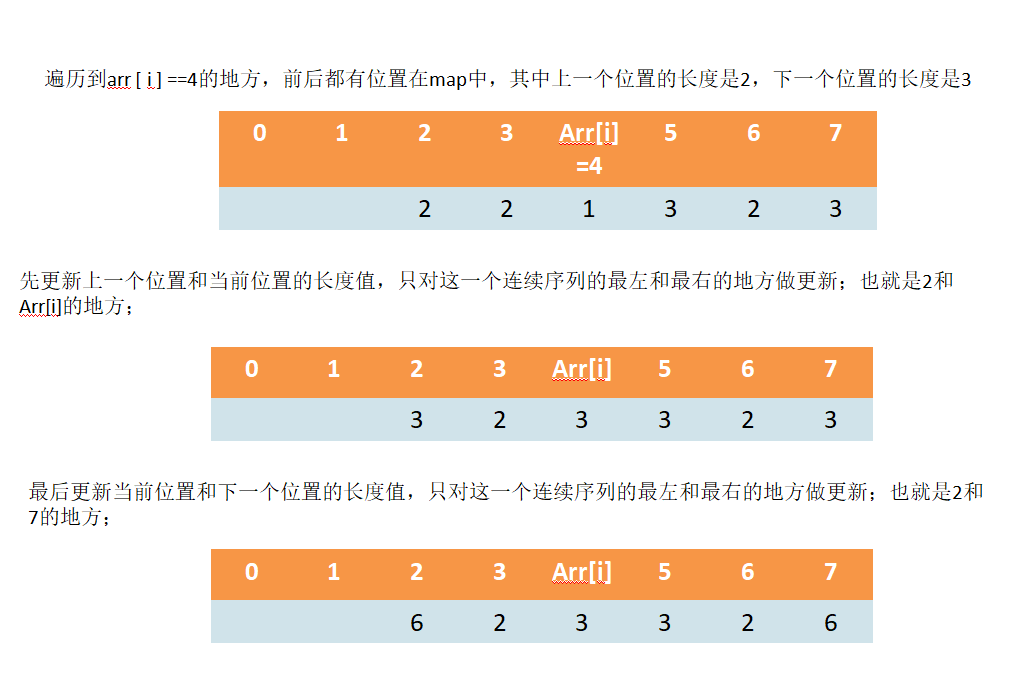
给定无序数组arr,返回其中最长的连续序列的长度(要求值连续,位置可以不连续,例如 3,4,5,6为连续的自然数
1
2
36
100 4 200 1 3 21
24
- 解析:1.对数组排序然后记录,2 . 哈希表实现:时间空间复杂度都是O(N);键为每一个数组中的数;值为该数作为连续序列的最长长度;但是用过的长度不在更新,只记录最左最右的部分;只需更新连续序列的最左和最右范围上的value:记录为该连续序列的长度。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
using namespace std;
/*
哈希表实现:时间空间复杂度都是O(N);键为每一个数组中的数;值为该数作为连续序列的最长长度;但是用过的长度不在更新,只记录
最左最右的部分;
只需更新连续序列的最左和最右范围上的value:记录为该连续序列的长度
*/
int longestConsecutiveSize(const vector<int> &arr)
{
if (arr.empty()) return 0;
map <int, int> table;
using pair_type = decltype(table)::value_type;
int Max = 1;
for (size_t i = 0; i < arr.size(); i++)
{
auto it = table.find(arr[i]);
if(it == table.end())
{
table[arr[i]] = 1;
auto pit = table.find(arr[i] - 1);
auto nit = table.find(arr[i] + 1);
if (pit != table.end())
{
int left = (arr[i] - 1) - table[arr[i] - 1] + 1; //前一个数的开端所在位置
//cout <<" left is " << left << endl;
//cout << " arr[i] " << arr[i] << " " << it->first << " " << it->second <<" " << table[arr[i]] <<endl;
int right = arr[i] + table[arr[i]] - 1; // 上一个为止的终端所在位置
//cout <<" right is " << right << endl;
int len = right - left + 1;
table[left] = len;
table[right] = len;
Max = max(len, Max);
}
if (nit != table.end())
{
int left = arr[i] - table[arr[i]] + 1;
int right = (arr[i] + 1) + table[arr[i] + 1] - 1;
int len = right - left + 1;
table[left] = len;
table[right] = len;
Max = max(len, Max);
}
}
}
/*
或者用下面两句得到最大值,而不去记录max
auto pr = max_element(begin(table), end(table),
[](const pair_type &p1, const pair_type &p2){return p1.second < p2.second;});
return pr->second;
*/
return Max;
}
int main ()
{
int n; cin >> n;
vector<int> arr(n, 0);
for(int i =0 ; i < n; i++)
cin >> arr[i];
cout << longestConsecutiveSize(arr) << endl;
}
龙与地下城游戏问题
给定一个二维数组map,含义是一张地图,例如,如下矩阵
游戏的规则如下:
1)骑士从左上角出发,每次只能向右或向下走,最后到达右下角见到公主。
2)地图中每个位置的值代表骑士要遭遇的事情。如果是负数,说明此处有怪兽,要让骑士损失血量。如果是非负数,代表此处有血瓶,能让骑士回血。
3)骑士从左上角到右下角的过程中,走到任何一个位置时,血量都不能少于1。为了保证骑土能见到公主,初始血量至少是多少?
根据map,输出初始血量。
1 | 3 3 |
- 解析:在下面的开始部分:
1 |
|
数字字符转化为字母组合的种数
给定一个字符串str,str全部由数字字符组成,如果str中的某一个或者相邻两个字符组成的子串值在1~26之间,则这个子串可以转换为一个字母。规定‘1’转换为“A”,“2”转换为“B”……”26”转化为“Z“。请求出str有多少种不同的转换结果,由于答案可能会比较大,所以请输出对10^{9}+7109+7取模后的答案。
2
3
4
5
5
能转换出来的结果有:“AAAAA”,“LAA”,“ALA”,“AAL”,“LL”。
解析:第三个解析最好:
(链接)[https://www.nowcoder.com/questionTerminal/6a5d7615332c49eb810c374dd6f37857?f=discussion]
这题使用动态规划的方法解决,主要是找到递推公式。用$f(n)$表示长度为$n$的字符串的有效组合数。
- 考虑这个字符串的末尾,有效的组合可以分为两类,一类是末尾是单个数字转化的,一类是末尾是两个数字转化的。
- 那么反过来就可以这样求 $f(n)$,先令$f(n) = 0$
- 如果字符串的最后一个数字可以转化为字母,我们就给$f(n)$加上$f(n-1)$,
- 如果字符串的最后两个数字可以转化为字母,我们就给$f(n)$ 加上$f(n-2)$。
1 |
|
字符串的交错组成
给定三个字符串str1、str2 和aim,如果aim包含且仅包含来自str1和str2的所有字符,而且在aim中属于str1的字符之间保持原来在str1中的顺序属于str2的字符之间保持原来在str2中的顺序,那么称aim是str1和str2的交错组成。实现一个函数,判断aim是否是str1和str2交错组成,如果是请输出“YES”,否则输出“NO”。
2
3
4
5
6
12
1AB2
YES
解析:
1
2
3
4
5
6
7
8先考虑空间复杂度为O(n, m)的dp[n+1][m+1];
1. dp[i][j]定义为str1[0..i-1]与str[0...j-1]是否可以交错组成aim[0...i+j-1];
2. dp[0][0]为空串与空串是否可以组成空串,为True;
3. dp[0][0..m-1]代表aim[0...m-1]能否只由串str2[0..m-1]组成;dp[0..n-1][0]代表aim[0..n-1]能否只由串str1[0..n-1]组成;
4. dp[i][j]的值由下组成:dp[i-1][j]代表aim[0..i+j-2]能否被str1[0..i-2]与str2[0...j-1]交错组成,如果再有
str1[i-1] == aim[i+j-1],说明str1[i-1]又可以作为aim[0...i+j-1]的最后一个字符,此时dp[i][j] = True;
dp[i][j-1]的分析与上面一样;
5. 除了满足4之外的dp[i][j]都为false;1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70/*
先考虑空间复杂度为O(n, m)的dp[n+1][m+1];
1. dp[i][j]定义为str1[0..i-1]与str[0...j-1]是否可以交错组成aim[0...i+j-1];
2. dp[0][0]为空串与空串是否可以组成空串,为True;
3. dp[0][0..m-1]代表aim[0...m-1]能否只由串str2[0..m-1]组成;dp[0..n-1][0]代表aim[0..n-1]能否只由串str1[0..n-1]组成;
4. dp[i][j]的值由下组成:dp[i-1][j]代表aim[0..i+j-2]能否被str1[0..i-2]与str2[0...j-1]交错组成,如果再有
str1[i-1] == aim[i+j-1],说明str1[i-1]又可以作为aim[0...i+j-1]的最后一个字符,此时dp[i][j] = True;
dp[i][j-1]的分析与上面一样;
5. 除了满足4之外的dp[i][j]都为false;
*/
bool isCompose(const string &s1, const string &s2, const string &aim)
{
if (s1.size() + s2.size() != aim.size()) return false;
vector< vector<int>> dp(s1.size() +1, vector<int>(s2.size() + 1, 0));
dp[0][0] = 1; //空串
for (int i = 1; i <= s1.size(); i++)
{
if (aim[i - 1] != s1[i - 1]) break;
dp[i][0] = 1;
}
for (int j = 1; j <= s2.size(); j++)
{
if (aim[j - 1] != s2[j - 1]) break;
dp[0][j] = 1;
}
for (int i = 1; i <= s1.size(); i++)
{
for (int j = 1; j <= s2.size(); j++)
{
if ( ((s1[i - 1] == aim[i + j - 1]) && dp[i - 1][j]) ||
((s2[j - 1] == aim[i + j - 1]) && dp[i][j - 1]))
dp[i][j] = 1;
}
}
return dp[s1.size()][s2.size()];
}
//化为空间复杂度只有最小串的长度+1,看出上面的dp【i】【j】计算只依赖上面的元素和左边的元素
bool isCompose2(const string &s1, const string &s2, const string &aim)
{
if (s1.size() + s2.size() != aim.size()) return false;
string more = s1.size() > s2.size() ? s1 : s2;
string less = s1.size() > s2.size() ? s2 : s1;
vector<int> dp(less.size() + 1, 0);
dp[0] = 1; //空串
for (int i = 1; i <= less.size(); i++)
{
if (aim[i - 1] != less[i - 1]) break;
dp[i] = 1;
}
for (int i = 1; i <= more.size(); i++)
{
dp[0] = dp[0] && more[i - 1] == aim[i - 1];
for (int j = 1; j <= less.size(); j++)
{
if ((more[i - 1] == aim[i + j - 1] && dp[j]) ||
(less[j - 1] == aim[i +j - 1] && dp[j - 1]))
dp[j] = 1;
else
dp[j] = 0;
}
}
return dp[less.size()];
}
int main()
{
string s1, s2, aim;
cin >> s1 >> s2 >> aim;
cout << (isCompose2(s1, s2, aim) ? "YES" : "NO") << endl;
}
排成一条线的纸牌博弈问题
给定一个整型数组arr,代表数值不同的纸牌排成一条线,玩家A和玩家B依次拿走每张纸牌,规定玩家A先拿,玩家B后拿,但是每个玩家每次只能拿走最左和最右的纸牌,玩家A和玩家B绝顶聪明。请返回最后的获胜者的分数。
2
2
3
1 2 100 4101
解析:
1
2
3
4
5
6
7
8
9
10
11
12
13/*
f(l,r) :表示arr[l...r]这个排列上的纸牌被先拿,最终的得分;
s(l,r) :表示arr[l...r]这个排列上的纸牌被后拿,最终的得分;
首先对于f方法来说,有两种拿法,要么先拿arr[l],要么先拿arr[r].
如果先拿arr[l],那么对于剩下的牌来说,拿到的最大分数就是arr[l]+s(arr, l+1, r)
如果先拿arr[r],那么对于剩下的牌来说,拿到的最大分数就是arr[r]+s(arr,l,r-1)
所以f(arr,l,r)的结果就是两者中的较大值.
同样的,对于s方法,也有两种拿法:
如果f方法已经拿去了arr[l],那么s方法得到的最大值就是f(l+1, r),
如果f方法已经拿去了arr[r],那么s方法得到的最大值就是f(l, r-1)
参考:
http://myblog.huangjinjin.xin/2018/11/27/%e6%9a%b4%e5%8a%9b%e9%80%92%e5%bd%92%e6%94%b9%e5%8a%a8%e6%80%81%e8%a7%84%e5%88%92%e5%a5%97%e8%b7%af2-%e7%ba%b8%e7%89%8c%e5%8d%9a%e5%bc%88%e9%97%ae%e9%a2%98/#comment-139
*/
1 |
|