前言:函数的增长
- 算法的渐进效率:我们关心当输入规模无限增加时,算法的运行时间如何随着输入规模的变大而增加。例子:输入规模$n$增大,最坏情况运行时间为$\Theta(n\lg n)$的归并排序战胜最坏情况运行时间为$\Theta(n^2)$的插入排序;
- 我们设最坏情况运行时间函数为$T(n)$;
- 算法分析的种类:
最坏情况(Worst Case):任意输入规模的最大运行时间。(Usually) 平均情况(Average Case):任意输入规模的期待运行时间。(Sometimes) 最佳情况(Best Case):通常最佳情况不会出现。(Bogus)
渐近记号(Asymptotic Notation)
渐进记号是应用于函数上的记号。
渐进记号刻画算法的运行时间,为了全面性(综合覆盖所有输入),提出了不同的渐进符号。
通常有 $O$、 $Θ$ 和 $Ω$ 记号法。$Θ$ 记号渐进地给出了一个函数的上界和下界,当只有渐近上界时使用 $O$ 记号,当只有渐近下界时使用 $Ω$ 记号。
尽管技术上 $Θ$ 记号较为准确,但通常仍然使用 $O$记号表示。
使用 $O$ 记号法(Big O Notation)表示最坏运行情况的上界。
如下的函数$f(n)$都是渐进非负的,也就是当$n$足够大,$f(n)$非负。
渐进记号出现在公式中,出现在等式右边,可以视为某一个不关心的匿名函数,如:
出现在等式左边,表示左边无论是什么匿名函数,右边总有一个匿名函数使得等式成立,例如:
前示
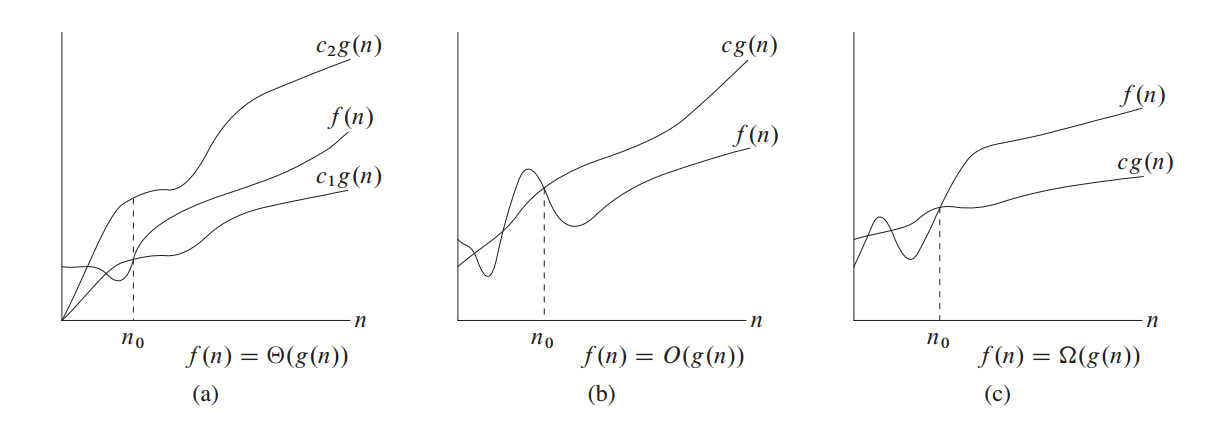
$\Theta$ 记号
定义:$\Theta(g (n))={f(n)$ :存在正常量$c_1,c_2,n_0 $使得对所有$n\ge n_0$,有$0 \le c_1g(n) \le f(n) \le c_2g(n)}$
$\Theta(g (n))$ 表示一个函数集合, $f(n)\in \Theta(g (n))$;
$g(n)$是$f(n)$的渐进紧确界。
$O$ 记号
定义:$O(g (n))={f(n)$ :存在正常量$c,n_0 $使得对所有$n\ge n_0$,有$0\le f(n) \le c g(n)}$。
只有一个渐进上界时,使用$O$记号。
$f(n)=O(g(n))$代表$f(n)\in O(g(n))$,因此$\Theta$是一个比$O$更强的概念,有$\Theta(g(n)) \subseteq O(g(n))$;
$\Omega$ 记号
定义:$\Omega(g (n))={f(n)$ :存在正常量$c,n_0 $使得对所有$n\ge n_0$,有$0\le c g(n) \le f(n) }$。
只有一个渐进下界时,使用$\Omega$记号。
$o$ 记号
是一个非渐进紧确的上界。
定义: $o(g (n))={f(n)$ :存在正常量 $c$,存在常量 $n_0$,使得对所有 $n\ge n_0$,有 $0 \le f(n) < cg(n) }$。
也就是说当$n$趋于无穷时, $g(n)$比$f(n)$大至少一个数量级。
引入的原因:$O$ 提供的渐进上界可能是也可能不是渐进紧确的。例子:$2n=O(n^2)$不是渐进紧确的。
$\omega$ 记号
是一个非渐进紧确的下界。
定义: $\omega(g (n))={f(n)$ :存在正常量 $c$,存在常量 $n_0$,使得对所有$n\ge n_0$,有$0\le cg(n) < f(n) }$。
也就是说当$n$趋于无穷时, $f(n)$ 比 $g(n)$大至少一个数量级。
comlexity table
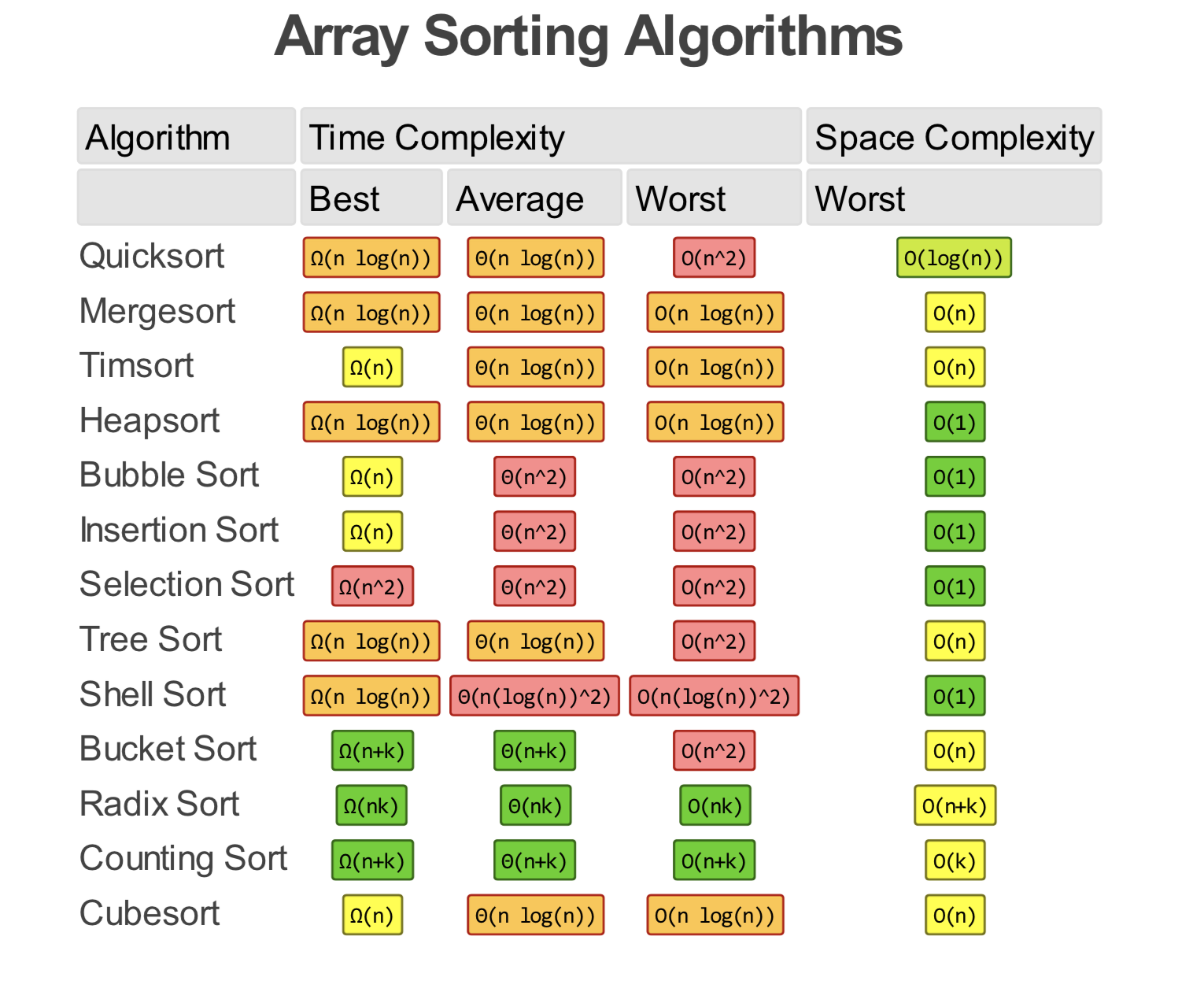
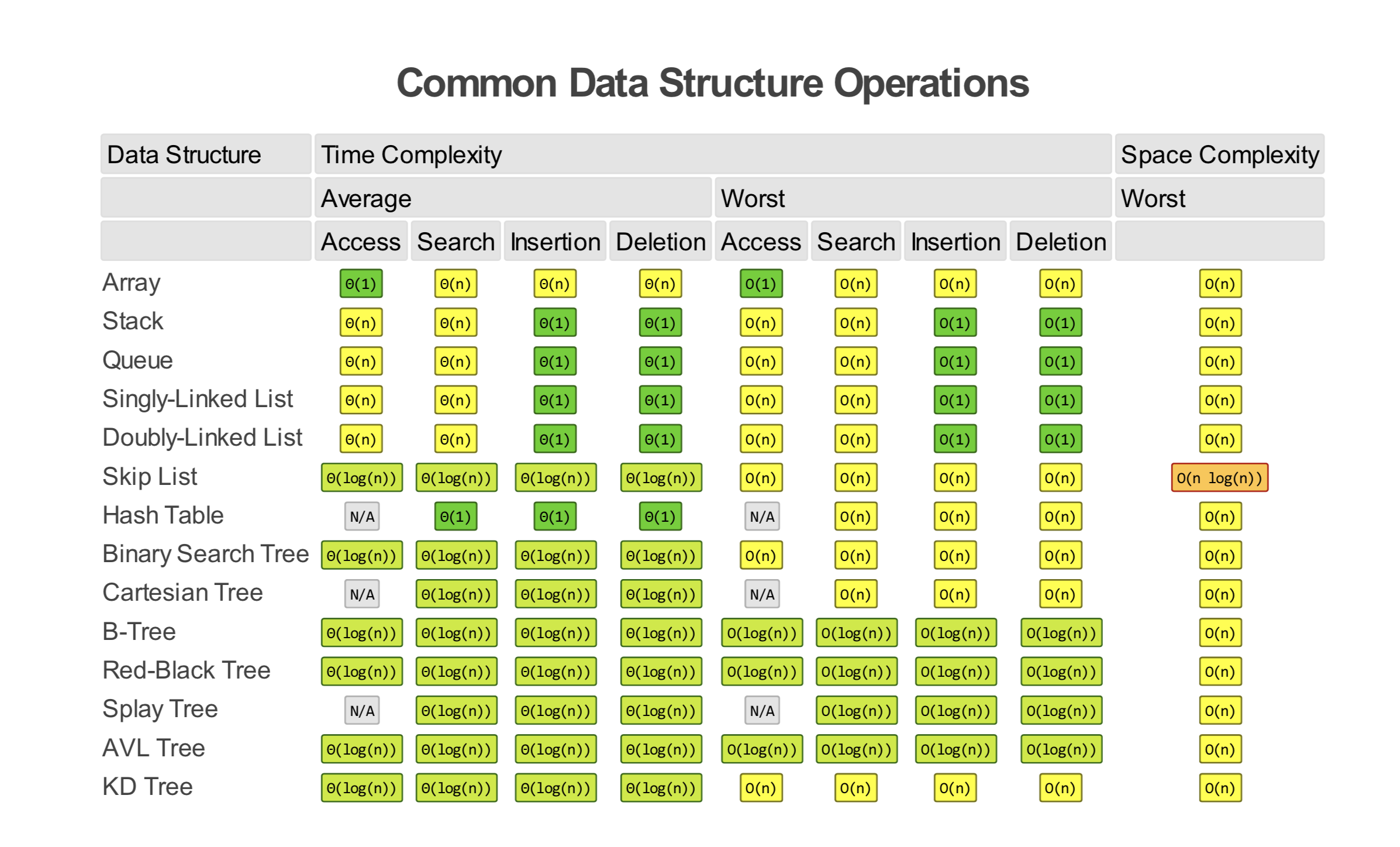
Reference:算法导论